Storing Data in Node-Red Variables

Node-red nodes pass the msg object between nodes.

However this object is replaced by the next msg object. So how do you store data between node calls?

Node-Red provides three mechanisms:

• The context object -stores data for a node
• The Flow object – stores data for a flow
• The global object -stores data for the canvas

I will illustrate these methods using a simple flow like the one below.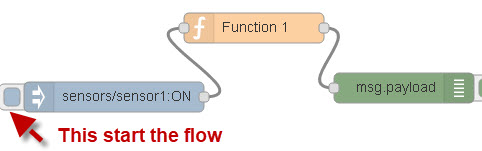

The inject node is used to start the flow , then function node implements the counter and the debug node displays the result.

The idea is to count the number of times the message was injected.

The actual message that gets injected isn’t important.

Note: There is a video to accompany this tutorial as it is easy to demonstrate the interaction between variables using video. You may want to read quickly through the text and then go to the video. Here is the video

Using the Context Object

This is used for storing function variables.

The process for retrieving and storing is to use the get method of the object for retrieving value and the set method to store values.:

name =context.get("name"); //to retrieve a variable  
context.set("name",name); // to store a variable

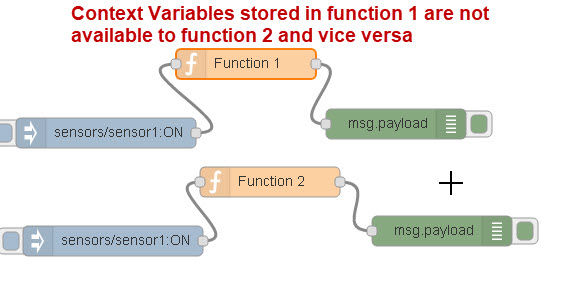
A variable stored for function 1 in the context object is not available to function 2 and vice versa.

Initialising the Variable

The standard way is to include this code at the top of the script:

var count=context.get('count') || 0;

Which means- If count doesn’t exist in the context object then make our local variable count zero; otherwise assign the stored value to our local variable count.

You can use multiple variables e.g.

var count=context.get('count') || 0;
var count2=context.get('count2') || 0;

You can also use an array or an object e.g

var local=context.get('data') || {};
if (local.count===undefined) //test exists
{
  local.count=0;
}

In the code above data is an object stored in the context object and local is our local object.

Here is an example script that uses a single variable as a counter in function 1:

var count=context.get('count') || 0;
count +=1;
msg.payload="F1 "+msg.payload+" "+count;
context.set('count',count);
return msg;

Note the above syntax is commonly seen on the Internet but it does cause strange problems due to the way JavaScript identifies True and False.

There instead of

var count=context.get('count') || 0;

I prefer to use this format:

var count=context.get('count') ;
if (typeof count=="undefined")
count=0;

Here is an example script that uses a object variable as a counter in function 2::

var local=context.get('data') || {};
if (local.count===undefined)//test exists
{
  local.count=0;
}
local.count +=1;
msg.payload="F2 "+msg.payload+" "+local.count;
context.set('data',local);
return msg;

If you look at the code for function 1 and function 2 you will see that they use the same counter variable..

However when you click the inject node for function 1 you see the counter value is 1 and then the inject node for function 2 then counter is also 1.

This shows that the counters are local to each function and not shared between functions.

Note: Currently if you restart the flow the variables are reset but this is likely to change.

Using the Flow Object

You use the flow object in the same way as the context object.

To retrieve values stored in the flow object use:

var count=flow.get('count') || 0;

and to store values use:

flow.set('count',count);

This time you should notice that the functions can share variables stored in flow objects. See video

Using the Global Object

You use the flow object in the same way as the context object.

To retrieve values stored in the flow object use:

var count=global.get('count') || 0;

and to store values use:

global.set('count',count);

This time you should notice that the functions can share variables stored in the global object even across flows.

Video -How to Store Data in Node-Red Variables

Flows Used in the video

Storing and Retrieving Multiple Variables

In node-red version 0.19 it became possible to store and retrieve several variables at once. So instead of using:

var v1=flow.get("v1");
var v2=flow.get("v2");
//You can use
var values=flow.get(["v1","v2"]);
var v1=values[0];
var v2=values[1];
//and
flow.set("v1",v1);
flow.set("v2",v2);
//You can use
flow.set(["v1","v2"],[1,2]);

If you look at the variables in the store you can see that they are stored as individual variables as shown in the screen shot below. The screen shot also shows how an variable array (data) is stored:

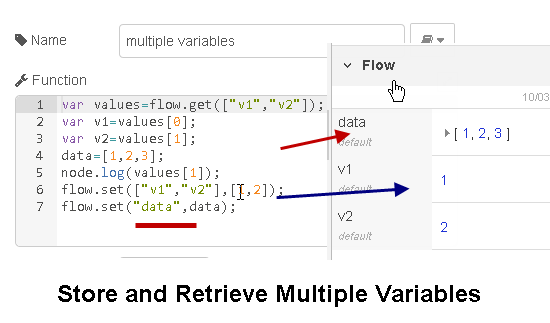
Storing Context Data in The File System

Data stored in the context,flow and global variables is known as context data and it is normally stored in memory.

This means that if you restart the flow then the data is lost.

However from version 0.19 it is possible to store the context data in the file system.

In order to do this you will need to modify the settings file and add the following entry:

contextStorage: {
   default: "memoryOnly",
   memoryOnly: { module: 'memory' },
   file: { module: 'localfilesystem' }
},

It doesn’t matter where in the settings file you place it and depending on the version of node-red you started with you may already have an entry that is commented out.

The settings above configure node-red to use the default store in memory and also the file system for the file store.

We therefore have two stores.

When saving data to the context variables or retrieving data from them you will need to specify the store they are in. The default is in memory.

So if you use:

var count=context.get("count");

You will retrieve the count variable from memory and to get the count variable from the file store use:

context.get("count", "file");

To store data use:

context.set("count", count,"file");

The system stores the variables in a JSON file in a folder called context under the .node-red folder.

Even though you are storing data in the file system it is still possible to loose data as the data is only flushed to the file system every 30 seconds.

You can change this (no real need) and other configuration options see the docs here.

You should also note that you can have two variables with the same name but stored in memory and file system as shown in the screen shot below:

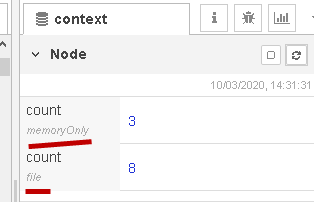
If you have multiple context stores then when using nodes like the change node you will be presented with a choice as shown below:

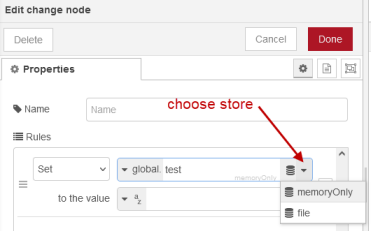
However you may want to only use the file store and to avoid confusion it is then easier to only enable that option by removing then memory option in the settings.js file as shown below:

contextStorage: { default: "file",
file: { module: 'localfilesystem' } },

You should be very careful when using multiple stores as it makes flows difficult to debug.

Exchange Data Between Nodes Without Wires

With node-red messages are usually passed between nodes using wires.

However it is possible to pass data between nodes with them being wired together using flow and global objects.

Video- Moving Messages between Flows Without Wires

Related tutorials

• Using Environmental Variables
• Understanding the Node-Red Message object
• Using the Node-Red Function Node- Beginners Guide
• Working with JSON data in Node-Red
• Initialising Node-Red Flows
• Understanding and Using Buffers In Node and Node-Red